Effects of radiation pressure and Earth’s oblatness on high altitude artificial satellite orbit

Khalil I. Khalil,¹ Mohamed N.S. Ismail²

¹National Research Institute of Astronomy and Geophysics, Cairo; ²Astronomy Department, Faculty of Science, Al-Azhar University, Cairo, Egypt

Correspondence: Dr. Mohamed N.S. Ismail, Astronomy Department, Faculty of Science, Al-Azhar University, Yosief Abbas Street, Cairo, Egypt. Tel. +20.2.2623274 - Fax. +20.2.2611404.
E-mail: mnader_is@yahoo.com

Key words: radiation pressure, artificial satellite orbits, perturbation technique, tesseral and zonal harmonics.

Received for publication: 8 August 2010.
Accepted for publication: 1 February 2011.

This work is licensed under a Creative Commons Attribution 3.0 License (by-nc 3.0).

©Copyright K.I. Khalil and M.N.S. Ismail, 2010
Licensee PAGEPress, Italy
Astronomy Studies Development 2011; 1:e2
doi:10.4081/asd.2011.e2







Introduction

Several models have been constructed in order to describe Earth’s gravitational field. Both of them aim at achieving a more accurate description of the Earth's spherical harmonics. For such complex force models, analytical solutions depicting the satellite orbital motion are more complicated. These solutions appear as a manifold of large domain of initial conditions and parameters.
On the other hand, numerical integrations are widely used methods providing a very accurate ephemeris of a satellite orbital determination. These methods ensure a reasonable accuracy comparable with that of analytical solutions. Therefore, the description of the satellite motion in the Earth’s gravitational field by an analytical theory ensuring comparable accuracy with that of numerical integration is seemed to be a reasonable task.
Stern1,2 and Cook et al.3 had generated analytical solutions for near Earth low eccentricity orbits. Kampos4 carried out an extension of the work reported by Kalil5 with the same atmosphere model. King-Hele and Walker6 extended the solutions to high eccentricity orbits. Engels and Junkins7 and Jezewski8 as well evolved analytical solutions with J2 for short-term orbit. However, the numerical integration methods provide more accurate ephemeris of a satellite with respect to any type of perturbing forces.9,10,11
It is well known that the solutions of the classical Newtonian equations of motion are not suitable for long-term integration. Many transformations have emerged in the literature in the recent past to stabilize the equations of motions either to reduce the accumulation of local numerical errors or allowing the use of larger integration step sizes, in the transformed space or both. Examples of such transformations include the use of a new independent variable, time transformation to orbital parameter space, which tends to decouple fast and slow variables, and the use of integrals as control terms. One such transformation, known as the KS transformation, is due to Kustaanheimo and Stiefel,12 who regularized the nonlinear Kepler motion and reduced it to linear differential equations of a harmonic oscillator of constant frequency.
Stiefel and Scheifele13 further developed the application of the KS transformation to problems of perturbed motion, producing a perturbation equations version. Kozai14 showed that a satellite theory, accurate to 5 m level for a low altitude case requires that the short periodic motion caused by first order and second order oblateness (J2, J2²), higher degree zonal harmonics (Jn, n>2), tesseral harmonics, and drag perturbations must be included. Sharma and Raj15 satisfactorily integrated numerically another form of KS differential equations called KS uniform regular canonical equations with Earth’s zonal harmonics J2 to J36. Analytical expressions for short periodic motion with the dominating term J2 in terms of KS elements were generated by Sharma16 and included terms of fourth power in eccentricity.

Earth's gravity

The Earth’s gravitational potential is usually expressed as

(1)

where R is the equatorial radius of the Earth, µ=G Me is the product of the gravitational constant and the mass of the Earth, (r, γ, δ) are the geocentric coordinates of the satellite with γ measured east of Greenwich, Cnm and Snm are harmonic coefficients, Pn^m (sin δ) are associated Legendre polynomials.
Equation (1) was firstly derived by Kaula.17,18 The terms with m = 0 correspond to zonal harmonics, while the terms with 0<m <1 correspond to tesseral harmonics, and for m=n the terms of sectorial harmonics.
In the present treatment the field will be assumed represented by a series, truncated at n=5. The coefficients C21 and S21 are finished, the coefficients C10, C11, S11 will be zero. Both the tesseral and sectorial harmonics will be simply referred to as tesseral harmonics. Thus equation (1) can be written in the form

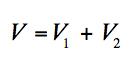(2)

where

(3)

(4)

where

Jn are the zonal harmonic coefficients, Pn (sin δ) is the Legendre polynomial, Pn^m (sin δ) is the associated Legendre polynomial, and

(5.1)

(5.2)

where

(6.1)

(6.2)

with

(7.1)

(7.2)

and r, a, e, Ω, ω, I are the radius vector, the semi major axis, the eccentricity, the longitude of ascending node, the argument of perigee, and the inclination of the orbital plane of the satellite respectively.
Let

(8.1)

(8.2)

Using equations (5), (6), (7) and (8) into equations (3) and (4) the zonal and tesseral terms in the Earth’s potential can be expressed in the form

(9.1)

(9.2)

Radiation pressure

The direct effect of the solar radiation on the satellite means the net acceleration resulting from the interaction (i.e. absorption, reflecting, or diffusion) of the sun light with each elementary surface of the spacecraft. Each photon carries an amount of momentum given by

(10)

Where Mom is the photon momentum, Eg is the energy of the photon ( proportional to the photon frequency), and C is the velocity of light. The momentum can be exchanged during interaction with a solid surface. So, the light behaves like a medium of material particles continuously emitted by the sun.
A satellite whose surface has a reflection coefficient α, placed at a distance d from the sun and receiving the solar radiation at an angle of incidence χ will experience an acceleration under the influence of solar radiation pressure, determined by

(11)

(12)

Where E0 is the solar constant, C is the speed of light, as is the mean distance Earth-Sun, and is a unit vector in the direction Earth-Sun given, in a geocentric equatorial frame by

(13)

Where As is the true celestial longitude of the Sun and ε is the obliquity of the ecliptic, As is expressed in terms of the orbital elements as As =fs+ωs. Due to the Earth’s shadow, is distance continuous function of time. With sufficient accuracy we can assume that:
i) The sun moves in a circular orbit such that As becomes the mean longitude of the Sun ν t+constant.
ii) The direction and distance of the satellite from the Sun are similar to those of the Earth.
The radiation pressure force may then be written as

(14)

Assuming suitable averages of A and χ; β^'1 may be considered constant.

The KS transformation

This transformation was suggested by Stiefel and Scheifele,13 the independent variable is changed from t (the ordinary time) to s (the fictitious time) through the Equation

(15)

and the dependent variable x is changed to a four vector u (the four dimensional parametric space), i.e.

(16)

where

(17)

Then, the vector (x1, x2, x3, 0) is transformed to

(18.1)

(18.2)

(18.3)

The equation of motion

It is known that the equation of motion of an artificial satellite under the effect of a perturbation force is given by

(20)

where
V is the perturbing potential depending on time and the position of the satellite, including the a sphericity of the earth, and is given by Equation (2)
is the perturbing force produced by the direct radiation pressure of the sun, and defined by equation (14).
Using the KS variables given in equations (17) and take into account that

(21)

where h is the total energy, substituting into equation (20), then, after some little reductions we have

(22.1)

(22.2)

(22.3)

(22.4)

Equations (22) are the equations of motion.

Numerical solution and application

The zonal and tesseral harmonics of the Earth potential, and the radiation pressure force are taken into account to solve the equations of motion (22). This would give ten ordinary differential equations, which could be solved by fourth order Runge Kutta method of integration. A Code was constructed using the Mathematica (version 7) to solve these equations. α’s, β’s, ω, and τ are obtained which are used to obtain the orbital elements. Then the effects on the orbital elements of the satellite due to the radiation pressure, the tesseral and zonal harmonics of the Earth’s gravitational potential could be obtained. The application is done for the high altitude artificial satellite Lageos-1 (Table 1) (http://www.space-track.org/perl/login.pl). Our results were congruent to the observations, and gave more accuracy than the previous works. Sehnal19 found that this effects were of order 10^–9, Liu20 found that the effects of the zonal harmonics are of order J2², our results was 2.3x10^–6 i.e. J2².We noted that the results of all other works in such method (KS) give a good results such as Sharma,16 and our results was an agreement with observations, such that the order of perturbations due to radiation pressure and the potential of Earth’s gravity is about 10^–6, that means of order J2². Figures 1a, b, c illustrate the perturbation effects on the semi-major axis, eccentricity, and inclination respectively during one day, Figures 2a, b, c illustrate the same perturbation effects during 150 days, while Figures 3a, b, c show the same effects during 600 days.

Table 1. The orbital elements of satellite Lageos-1.

Figure 1. (a) The perturbations effects on semi major axis during one day. (b) The perturbations effects on eccentricity during one day. (c) The perturbations effects on inclination during one day.

Figure 2. The perturbation effects during 150 days. (a) Perturbation effects on semimajor axis during 150 days. (b) Perturbation effects on eccentricity during 150 day. (c) Perturbation effects on inclination during 150 days.

Figure 3. The perturbation effects during 600 days. (a) Perturbations effects on semi-major axis during 600 days. (b) Perturbations effects on eccentricity during 600 days. (c) Perturbations effects on inclination during 600 days.

Conclusions

We concluded that
i. The KS variables are used to regularize the equation of motion of the artificial satellite. This regularization is used only for the numerical solutions methods, but not for the analytical solutions.
ii. The Runge Kutta numerical integration method of fourth order is a suitable method for the transformations depend on the KS variables, and give a good accuracy.
iii. Although the tesseral effects are (of order J2²), but must be taken into account with the zonal effects (order J2 andJ2²).
iv. Effects due to radiation pressure, and gravitational potential of the Earth together on high altitude satellites orbit are of order (J2²). In the near future the effects of the Earth’s shadow will be taken into account. And in more complicated work the indirect radiation pressure (albedo) effects will be studied in details.

References

1. Stern TE. The effect of the rotation of a planetary atmosphere upon the orbit of a close satellite. Astron J 1959;64:54.[Abstract]
2. Stern TE. An introduction to celestial mechanics. 1960, Interscience Publ., Inc, New York, NY, USA.
3. Cook GE, King-Hele DG, Walker DMC. The Contraction of Satellite Orbits Under the Influence of Air Drag. II. With Oblate Atmosphere. Proc R Soc London A 1961;264:88-121. [Abstract]
4. Kampose B. General perturbation theory. 1968, NASA CR 1008.
5. Kalil F. Effect of an oblate rotating atmosphere on the eccentricity, semi major axis and period of a close Earth satellite. 1968, The Martin Company, Baltimore, MD, USA.
6. King-Hele DG, Walker DMC. The contraction of satellite orbits under the influence of air drag. VII. High eccentricity orbits, with scale hight dependent on altitude. Proc Soc Lond A 1987;411:1-17.[Abstract]
7. Engels RC, Junkins JL. The gravity perturbed Lambert problem: a KS variation parameters approach. Celestial Mech Dyn Astron 1981;24:3-21.[Abstract]
8. Jezewski DJ. A non canonical analytical solution to J2 perturbed two body Problem. Celestial Mech Dyn Astron 1983;30:343-61.[Abstract]
9. Merson RH. Numerical integration of the differential equations of celestial mechanics. REATR 74185.
10. Graf OF Jr., Mueller A, Starke S. The method of averages applied to the KS 10. differential equations. 1977, NASA-CR-151607.
11. Sharma RK, Mani L. Study of RS-1 orbital decay with KS differential equations. Indian J Pure Appl Math 1985;6:833-42.[FullText]
12. Kustaanheimo P, Stiefel EL. Perturbation theory of Kepler motion based on spinor regularization. J Reine Angew Math 1965;218:204-19.[Abstract]
13. Stiefel EL, Scheifele G. Linear and Regular Celestial Mechanics. 1971, Springer-Verlag, Berlin, Germany.
14. Kozai Y. The stability of the Solar System and of Small Stellar Systems. D. Reidel Publ. Co., Inc., Boston, MA, USA.
15. Sharma RK, Raj MXJ. Long-term orbit computations with KS uniformly regular canonical elements with oblateness. Earth Moon Planets 1988;42:163-78.[Abstract]
16. Sharma RK. Contraction of high eccentricity satellite orbits using KS elements with air drag. Proc. R. Soc. London A 1998;438: 467-75.[Abstract]
17. Kaula WM. Analysis of Gravitational and Geometric Aspects of Geodetic Utilization of Satellites. Geophysics J Int 1961;5:104-33.[Abstract]
18. Kaula WM. Theory of Satellite Geodesy. Applications of Satellites to Geodesy. 1966, Blaisdell Publ. Co., Waltham, MA, USA.
19. Sehnal L. Space Project Mimosa. Publ Astron Obs Belgrade 2003;75:195-208.[FullText]
20. Liu L., Liao, X. Numerical calculations in the orbital determination of an artificial satellite for a long arc. Celestial Mech Dyn Astron 1994;59:221-35. [Abstract]

[TOP]